How To Find Lcm And Hcf Using Prime Factors
Using Prime number Factorization to Find LCM
From my previous lesson, I went over the steps on how to find the LCM of two positive integers using the Listing Method. This time I will focus on the method where Prime Factorization is used to notice the LCM.
I highly recommend that yous review the procedure on how to perform Prime Factorization because this skill volition play a major role in this lesson. Check out the following link: Integer Prime Factorization.
Steps on How to Find the LCM using Prime Factorization
Step 1: Perform the prime factorization of each number then write it in exponential class. Marshal the common prime cistron base of operations whenever possible.
Step 2: For the numbers with a common prime gene base, select the prime number that has the highest power. The prime gene with the highest power implies that it occurs the virtually in the entire list.
Stride 3: If a distinct prime factor has NO matching prime cistron base of operations in the list, immediately include this cistron with its exponent in the collection of numbers that yous volition multiply after.
Annotation: Steps #2 and #iii ensure that all distinct prime factors in the Entire list are represented without duplicates.
Step 4: To make up one's mind the To the lowest degree Common Multiple (LCM), multiply all the numbers that you have collected or gathered from steps #two and #three.
Examples of Determining the Least Common Multiple (LCM) using Prime number Factorization
Example 1: What is the LCM of 12 and xc?
First, write the prime factorization of each number in exponential form. Brand certain to align the numbers that accept a mutual base. If a number does non have a common base of operations, then write information technology in a way that there's nothing above or below it to indicate that it is unique.
Observe that {2^2} and 2 are vertically aligned to signify they accept a common base of 2. In the aforementioned manner, 3 and {3^ii} are aligned because they have a common base of iii. Nevertheless, five has a unique base and so we write it by itself on its own "cavalcade".
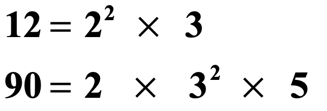
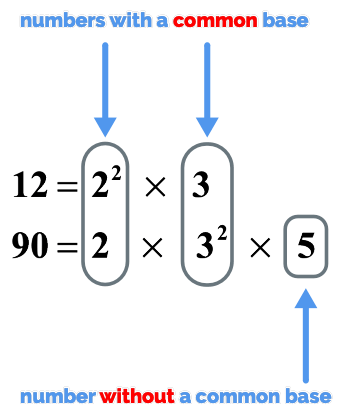
For emphasis, I labeled the prime factorizations of 12 and 90. I hope it makes a lot more sense now.
Now, it is fourth dimension to choose the numbers that nosotros are going to multiply to get the LCM.
- First, between {2^2} and 2, we will select {2^2} because it has a higher power than 2.
- Secondly, between three and {iii^2}, we choose {three^ii} for the same reason.
- Finally, since the base 5 is past itself and we have nothing to compare it with, we will automatically select it to be included in the group.
- Therefore, the numbers that we are going to multiply to determine the LCM of 12 and ninety are {ii^2}, {3^ii} and {5}.
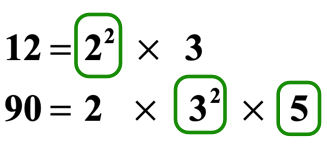
- Multiplying the numbers we have selected, we go:
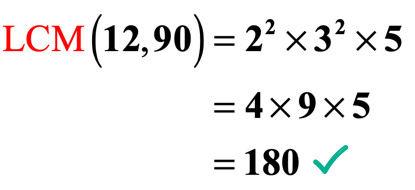
Example 2: What is the LCM of 80 and 120?
This time the numbers are relatively larger than in the previous example. Nonetheless, don't fret because as long every bit you stick to the process, the entire solving procedure for LCM is going to exist polish sailing. That's a testament to the ability of prime number factorization. Information technology doesn't affair how large the integers are because they can be expressed equally prime factors.
Every bit you may take already observed, existence able to correctly prime number factorize a positive integer is an indispensable skill to acquire and main. Once y'all have it, nobody can have it away from yous.
Begin by prime factorizing 80 and 120. Observe that the numbers with bases of 2 and v are respectively aligned vertically. The prime factor 3 is by itself so in that location'southward no number above it.
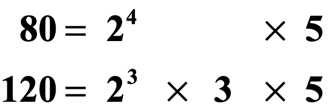
Beneath is the same image but with labels for emphasis.

Allow'due south pick the numbers to multiply to determine the to the lowest degree mutual multiple.
- Between {2^iv} and {ii^3}, we selection {2^four} over {ii^3} considering the former has a higher power than the latter since 4 > 3.
- The number three is by itself and so we will automatically include it in the collection of numbers that we are going to multiply.
- The numbers 5 and 5 are exactly the same. Nosotros will just pick i copy of 5 to correspond the two.
- Therefore, the numbers {2^iv}, iii, and 5 are the ones we will multiply to the LCM of
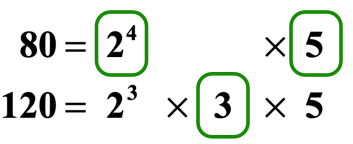
- And so the LCM for lxxx and 120 is calculated equally follows:
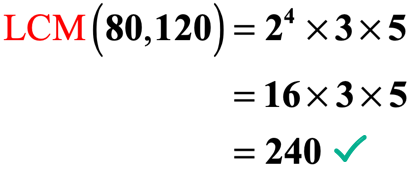
Example three: What is the LCM of 17 and 71?
Don't rush into solving the problem because you are already familiar with the steps. It wouldn't hurt to footstep dorsum for a moment to wait at the problem in a bigger picture.
In this instance, you should be able to spot immediately that both 17 and 71 are prime numbers. Remember that a prime number is but divisible by 1 and itself. Just a quick reminder, don't forget the fact that the smallest prime number is ii and Non ane.

So if nosotros are going to perform prime factorizations on a prime number, you should exist convinced that the prime factorization of a prime number is just the prime number number itself. Please don't include ane since information technology is not a prime number.
Hither are the prime number factorizations of the prime numbers 17 and 71. I didn't align them in the same column because they don't have a common base.
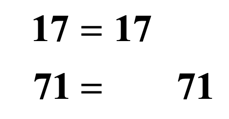
The adjacent obvious step is to cull the numbers that we are going to multiply. Since the bases are different from each other then we must select both of them.
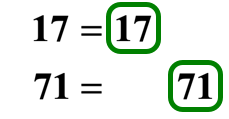
To find the LCM of 17 and 71, we have:
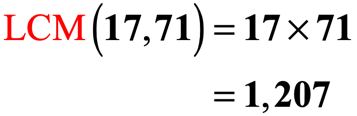
Example 4: What is the LCM of 126, 252, and 336?
Let's kicking information technology upwardly a notch by finding the least common multiple (LCM) of three distinct positive integers that are in the hundreds.
I know that it can be intimidating because it feels like we are in a new territory. However, if you lot are already familiar with prime factorization in that location is naught you should worry about. You got this!
The steps or procedures in finding the LCM of 3 integers are very similar to finding the LCM of two numbers which at this signal you should take a mastery already.
Get-go by applying Prime Factorization on the positive integers 126, 252, and 336. Again, it is and then important that we align the numbers that have a common base. As you tin can find, we vertically aligned the numbers with a base of 2, a base of three, and a base of seven. This uncomplicated trick gives united states enormous heads up on what to do side by side.
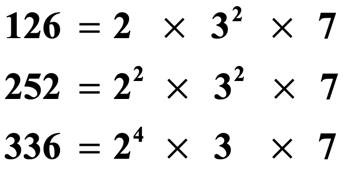
The post-obit illustration only emphasizes the fact that nosotros aligned the numbers that take the same base of operations.
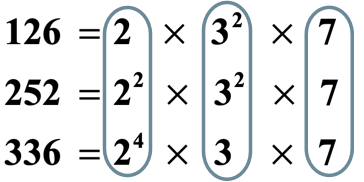
The next step every bit you already know is to select the numbers that we are going to multiply to determine the least mutual multiple of the three numbers.
- With a common base of 2, nosotros select {ii^4} since it has the highest power.
- With a common base of iii, we select {three^2} because information technology has the highest ability. Since there are ii {three^ii}, only option 1 instance of it.
- With a mutual base of seven, we select 7 considering they are withal.

The least common multiple (LCM) of 126, 252, and 336 is the product of the numbers that we take selected in a higher place. They are marked in orange.
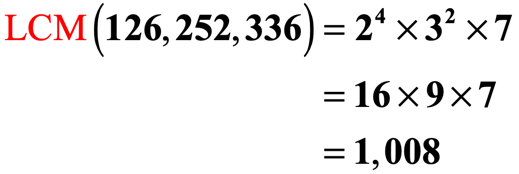
You might also exist interested in:
Finding LCM using the List Method
Finding GCF using the List Method
Utilize Prime Factorization to Find GCF
How To Find Lcm And Hcf Using Prime Factors,
Source: https://www.chilimath.com/lessons/introductory-algebra/use-prime-factorization-to-find-lcm/
Posted by: zaratenowbod.blogspot.com


0 Response to "How To Find Lcm And Hcf Using Prime Factors"
Post a Comment